Algebraens fundamentalteorem

TMA4400 Matematikk 1: Kalkulus og lineær algebra

Dato: 18. august 2025

Teorem. Enhver ligning på formen

\[ z^n + a_{n-1} z^{n-1} + \cdots + a_2 z^2 + a_1 z + a_0 = 0, \]

der \(a_{n-1}, \ldots, a_0\) er vilkårlige komplekse tall, har en løsning.

Husk polarform: \(z = r e^{i \varphi}\).

Vi utforsker hva som skjer på venstre siden av ligningen over når \(r\) er fast, men \(\varphi\) varierer fra \(0\) til \(2 \pi\). Vi kan prøve det visuelt med hjelp av den følgende python-koden.

import numpy as np
import matplotlib.pyplot as plt

# vårt polynom
def f(z):
    return z**4 + 1j * (z**3) + 1j * (z**2) + 2j*z - 1

# 1000 punkter langs enhetssirkelen i det komplekse planet
phi = np.linspace(0.0, 2 * np.pi, 1000)
r = 1
MAX = 10

# litt pynting av outputen
fig, ax = plt.subplots()
ax.set_xlim(-MAX,MAX)
ax.set_ylim(-MAX,MAX)
ax.spines['left'].set_position('zero')
ax.spines['bottom'].set_position('zero')
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')

# plotte det komplekse punktet som kommer ut når vi setter r ext(i phi) inn i f
ax.plot(f(r * np.exp(phi * 1j)).real, f(r * np.exp(phi * 1j)).imag)

plt.show()

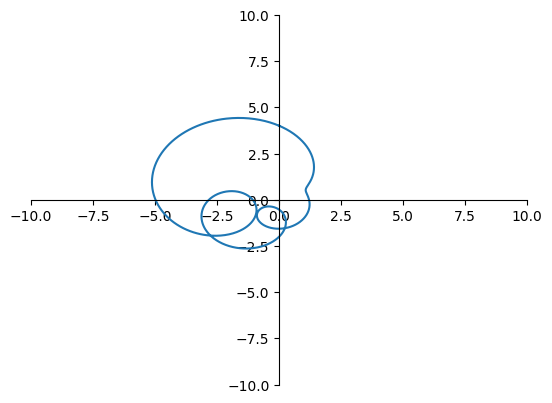
Observasjoner:

1. Hvis \(r\) er veldig liten så er det \(a_0\) som gir det største bidraget til resultatet.

2. Hvis \(r\) er veldig stor så er det \(z^n\) som gir det største bidraget til resultatet. Da går kurven rundt origo \(n\) ganger.

Vi kan visualisere overgang fra liten \(r\) til stor \(r\) i det følgende.

%matplotlib ipympl
# hvis det kommer uforstålige feilmeldinger så må du kanskje finne ut hvordan du kan laste ned ipympl
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.widgets import Slider

def f(z):
    return z**4 + 1j * z**3 + 1j * z**2 + 2j*z - 1

phi = np.linspace(0.0, 2 * np.pi, 1000)
MAX = 10

fig, ax = plt.subplots()
ax.set_xlim(-MAX,MAX)
ax.set_ylim(-MAX,MAX)
ax.spines['left'].set_position('zero')
ax.spines['bottom'].set_position('zero')
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
curve, = ax.plot(f(np.exp(phi*1j)).real, f(np.exp(phi*1j)).imag)

# slider for å kunne tilpasse r interaktivt
radius_ax = fig.add_axes([0.1,0.02,0.8,0.02])
radius_slider = Slider(ax=radius_ax, label='r', valmin=0, valmax=2, valinit=1)
radius_slider.on_changed(lambda val: curve.set_data(f(val * np.exp(phi*1j)).real, f(val * np.exp(phi*1j)).imag))

plt.show()

Kontinuerlig overgang fra et punkt til en kurve som går rundt origo \(n\) ganger krever at kurven på et tidspunkt underveis går gjennom origo. Det vil si vi finner en løsning for ligningen.