Taylors teorem

Contents

Taylors teorem#

TMA4400 Matematikk 1: Kalkulus og lineær algebra

Dato: 06. oktober 2025

Taylors teorem er gitt som:

Teorem. Anta at \(f(x)\) og dens deriverte av orden \(k\in\{1,2,\ldots,n+1\}\), \(f^{(k)}(x)\), er kontinuerlige på et åpent intervall \(I\) om punktet \(x=x_0\). Da er

\[ f(x)=f(x_0)+f'(x_0)(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2+\cdots+\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n+R_n(x),\qquad \text{for alle $x\in I$}, \]

hvor

\[ R_n(x)=\frac{f^{(n+1)}(c)}{(n+1)!}(x-x_0)^{n+1}, \qquad \text{for en $c$ mellom $x$ og $x_0$.} \]

La oss sjekke Taylors teorem geometrisk. For å gjøre dette implementerer vi litt python-kode.

Eksempel#

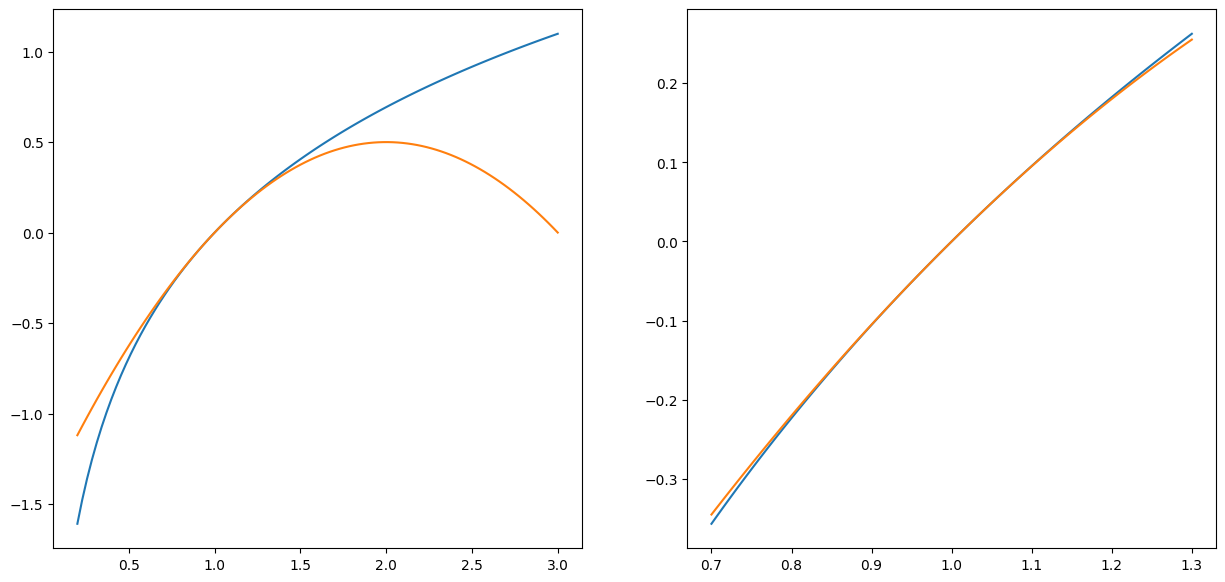
Finn en lineær tilnærming til \(f(x)=\log(x)\) om punktet \(x=1\).

Vi har at \(\log(1)=0\), \(f'(x) = \frac{1}{x}\) og \(f'(1)=1\).

Den linære tilnærmingen av \(\log(x)\) om punktet \(x=1\) blir altså

\[ \log(x) \approx x-1. \]
import numpy as np
import matplotlib.pyplot as plt

# 100 punkter mellom 0.2 og 3, for grafene til venstre
x = np.linspace(0.2,3,100)

# 100 punkter mellom 0.8 og 1.2, for grafene til høyre
y = np.linspace(0.8,1.2,100)

# log(x) på punktene mellom 0.2 og 3
f = np.log(x)
# log(y) på punktene mellom 0.8 og 1.2
g = np.log(y)

# lager figuren
fig, (ax1, ax2) = plt.subplots(1,2, figsize=(15,7))

# plottene til venstre, 0.2<x<3
# plotter y=log(x) i blå
ax1.plot(x,f)
# plotter y=x-1 i oransje
ax1.plot(x,x-1)

# plottene til høyre, 0.8<x<1.2
# plotter y=log(x) i blå
ax2.plot(y,g)
# plotter y=x-1 i oransje
ax2.plot(y,y-1)

[<matplotlib.lines.Line2D at 0x7f44b3194350>]
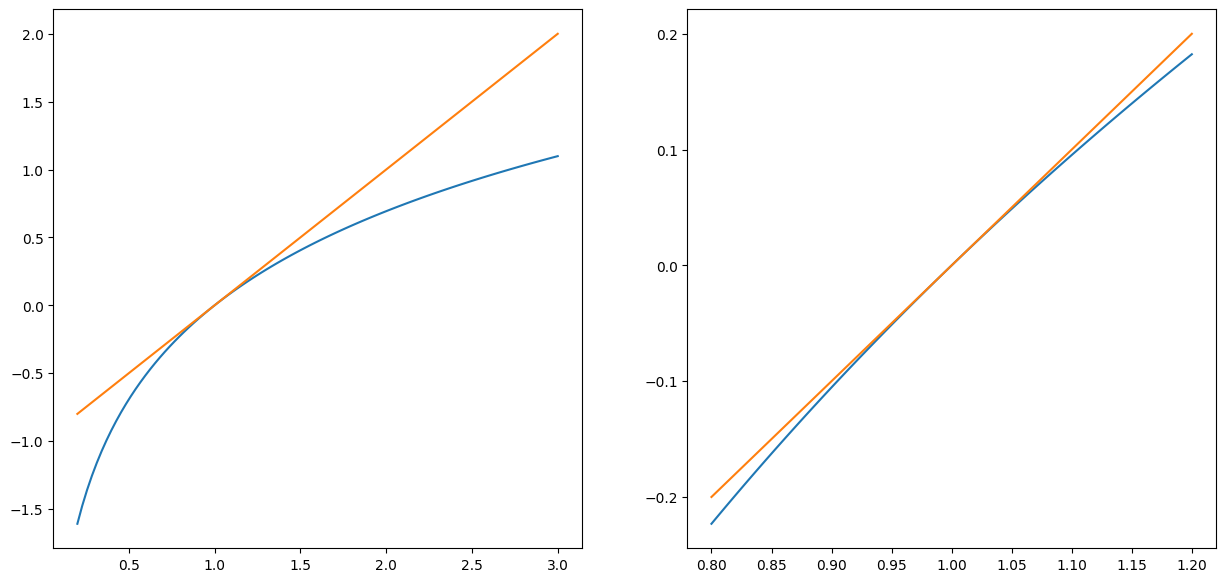
../_images/468879386a2c3f3d099cbbfe13a387977b2e794ed5057ea568dcc6fcb1dd4a8f.png

Eksempel#

La oss fortsette med \(f(x)=\log(x)\) om punktet \(x=1\).

Vi har \(f''(x) = -x^{-2}\), slik at \(f''(1)=-1\). Vi får derfor at

\[ \log(x) \approx (x-1) - \frac{1}{2}(x-1)^2. \]
# 100 punkter mellom 0.2 og 3, for grafene til venstre
x = np.linspace(0.2,3,100)
# 100 punkter mellom 0.7 og 1.3, for grafene til høyre
y = np.linspace(0.7,1.3,100)

# log(x) på punktene mellom 0.2 og 3
f = np.log(x)
# log(y) på punktene mellom 0.7 og 1.3
g = np.log(y)

# andreordens taylor tilnærming mellom 0.2 og 3
f2 = (x-1) - 0.5*(x-1)**2
# andreordens taylor tilnærming mellom 0.7 og 1.3
g2 = (y-1) - 0.5*(y-1)**2

# Lag figuren
fig, (ax1, ax2) = plt.subplots(1,2, figsize=(15,7))

# til venstre, 0.2<x<3
# log(x) i blå
ax1.plot(x,f)
# andreordens taylor i oransje 
ax1.plot(x,f2)

# til høyre, 0.7<x<1.3
# log(x) i blå
ax2.plot(y,g)
# andreordens taylor i oransje
ax2.plot(y,g2)

[<matplotlib.lines.Line2D at 0x7f44b0baefd0>]
../_images/2ddd57098ed31e81aee50ea588be631699d379391f3e61c98f8e926308d51a35.png
Contents