Numerisk derivasjon

TMA4400 Matematikk 1: Kalkulus og lineær algebra

Dato: 06. oktober 2025

For en funksjon \(f:D_f\to\mathbb{R}\) er den deriverte definert til å være

\[ f'(x)=\lim_{h\to0}\frac{f(x+h)-f(x)}{h}. \]

Vi ser derfor at

\[ f'(x)\approx\frac{f(x+h)-f(x)}{h}. \]

Eksempel

La \(f(x)=e^x\) og \(x_0=1.5\). Da er \(f'(x)=e^x\) og vi får følgende tabell:

\(h\)	\(f'(x_0)\)	\(\frac{f(x_0+h)-f(x_0)}{h}\)	\(\text{Feil}\)
\(10^{-1}\)	\(4.4817\)	\(4.7134\)	\(2\cdot 10^{-1}\)
\(10^{-2}\)	\(4.4817\)	\(4.5042\)	\(2\cdot 10^{-2}\)
\(10^{-3}\)	\(4.4817\)	\(4.4839\)	\(2\cdot 10^{-3}\)

Det er her tydelig at feilen er proposjonal med \(h\).

Numerisk derivasjon

Vi trenger litt hjelp fra Taylors teorem:

---

Teorem. Anta at \(f(x)\) og dens deriverte av orden \(k\in\{1,2,3,4\}\), \(f^{(k)}(x)\), er kontinuerlige på et åpent intervall \(I\) om punktet \(x=x_0\). Da er

\[ f(x)=f(x_0)+f'(x_0)(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2+\frac{f^{(3)}(x_0)}{3!}(x-x_0)^3+R_3(x),\qquad \text{for alle $x\in I$}, \]

hvor

\[ R_3(x)=\frac{f^{(4)}(c)}{4!}(x-x_0)^4, \qquad \text{for en $c$ mellom $x$ og $x_0$.} \]

---

Bytt nå ut \(x\) med \(x+h\) og \(x_0\) med \(x\) i teoremet over. Da ser vi at

\[ \frac{f(x+h)-f(x)}{h}-f'(x)=\frac{h}{2}f''(c), \]

eller

\[ |\text{Feil}|\leq \frac{h}{2}|f''(c)|\leq \frac{h}{2}\max_{x\in I}|f''(x)|\leq Ch. \]

Vi sier at vi har første ordens tilnærming av den deriverte når \(|\text{Feil}|\leq C h\).

Ved å kombinere Taylors teorem på ulike måter får vi for eksempel også at

\[ \frac{f(x+h)-f(x-h)}{2h}-f'(x)=-\frac{h^2}{12}\left(f^{(3)}(c_1)+f^{(3)}(c_2)\right). \]

Her vil altså \(|\text{Feil}|\leq C h^2\), eller andre ordens tilnærming av den deriverte. Og slik kan man fortsette for å få høyere ordens tilnærminger. Men jo høyere orden på tilnærmingen, jo høyere ordens deriverte trenger vi.

La oss teste teorien med litt koding i python.

import numpy as np
import matplotlib.pyplot as plt
import math

def f(x):                            # definerer funksjonen selv
    return math.exp(x)

def f_prime(x):                      # definerer den deriverte
    return math.exp(x)

def first_order(x_0, h):             # definerer første ordens approksimasjon
    return (f(x_0+h)-f(x_0)) / h

def second_order(x_0, h):            # definerer andre ordens approksimasjon
    return (f(x_0+h)-f(x_0-h)) / (2*h)

x_0 = 1.5                            # punktet vi er interessert i
actual = f_prime(x_0)                # faktisk verdi i dette punktet

print("Actual value " + str(actual))
print("============================================")

i = 0
divided_difference = np.zeros(4)
symmetric_difference = np.zeros(4)
error_d = np.zeros(4)
error_s = np.zeros(4)

for h in [0.1, 0.01, 0.001, 0.0001]: # vi lar h være mindre og mindre, men positiv
    
    print("h = " + str(h))

    divided_difference[i] = first_order(x_0, h)
    symmetric_difference[i] = second_order(x_0, h)
    error_d[i] = abs(divided_difference[i] - actual)
    error_s[i] = abs(symmetric_difference[i] - actual)
    
    print("Divided difference = {:>12}, Error = {:>12}".format(str(divided_difference[i]), str(error_d[i])))
    print("Symmetric difference = {:>12}, Error = {:>12}".format(str(symmetric_difference[i]), str(error_s[i])))
    print("============================================")
    
    i = i+1

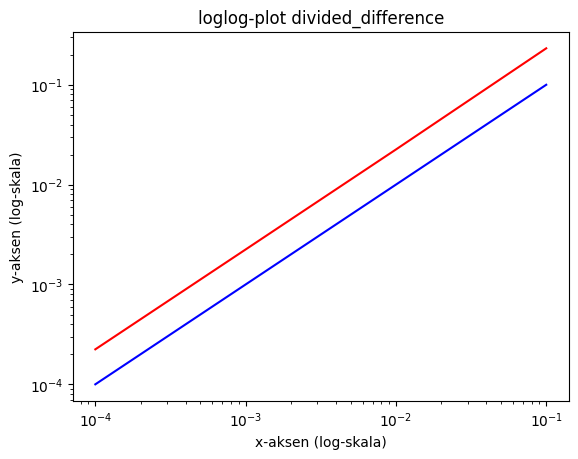
# vi ønsker nå å sjekke om ordenen til divided_difference faktisk er lineær

def g(x):                      # definerer den lineære funksjonen
    return x**1

# vi lager et loglog-plot hvor vi skal få rett linje dersom ordenen er lik 1
plt.loglog([0.1, 0.01, 0.001, 0.0001], error_d, 'r')
plt.loglog([0.1, 0.01, 0.001, 0.0001], [g(0.1), g(0.01), g(0.001), g(0.0001)], 'b')
plt.title('loglog-plot divided_difference')
plt.xlabel('x-aksen (log-skala)')
plt.ylabel('y-aksen (log-skala)')
plt.show()
    
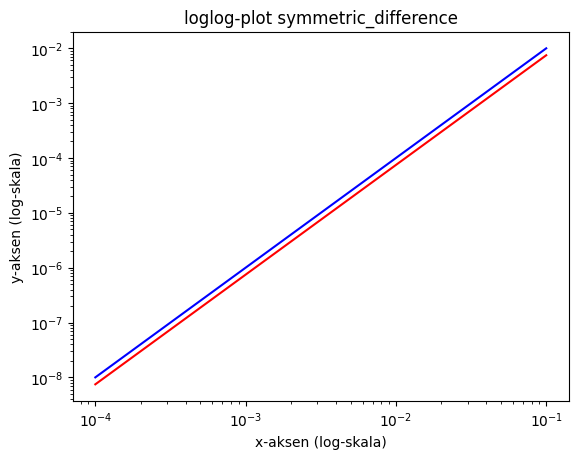
# vi ønsker nå å sjekke om ordenen til symmetric_difference faktisk er kvadratisk

def h(x):                      # definerer den kvadratiske funksjonen
    return x**2

# vi lager et loglog-plot hvor vi skal få rett linje dersom ordenen er lik 2
plt.loglog([0.1, 0.01, 0.001, 0.0001], error_s, 'r')
plt.loglog([0.1, 0.01, 0.001, 0.0001], [h(0.1), h(0.01), h(0.001), h(0.0001)], 'b')
plt.title('loglog-plot symmetric_difference')
plt.xlabel('x-aksen (log-skala)')
plt.ylabel('y-aksen (log-skala)')
plt.show()

Actual value 4.4816890703380645
============================================
h = 0.1
Divided difference = 4.713433540570504, Error = 0.2317444702324396
Symmetric difference = 4.489162287752202, Error = 0.007473217414137423
============================================
h = 0.01
Divided difference = 4.5041723976187775, Error = 0.022483327280713006
Symmetric difference = 4.481763765529401, Error = 7.469519133618263e-05
============================================
h = 0.001
Divided difference = 4.483930662008362, Error = 0.0022415916702973604
Symmetric difference = 4.481689817286139, Error = 7.469480740596168e-07
============================================
h = 0.0001
Divided difference = 4.481913162264206, Error = 0.00022409192614158968
Symmetric difference = 4.48168907780655, Error = 7.468485385686563e-09
============================================