Fikspunktiterasjoner

TMA4400 Matematikk 1: Kalkulus og lineær algebra

Dato: 15. september 2025

Røtter av ikke-lineære ligninger

Vi sier at \(x_0\) er en rot eller et nullpunkt til \(f(x)\) dersom

\[ f(x)=0. \]

En ikke-lineær ligning kan ha en, flere, eller ingen røtter.

Eksempel

Gitt funksjonen \(f(x)=x^2-2\) for \(x\in[-2,2]\). Skisser grafen til funksjonen ved å bruke følgende kode:

%matplotlib inline

# fikser litt på pyplot
import numpy as np
import matplotlib.pyplot as plt
newparams = {'figure.figsize': (8.0, 4.0), 'axes.grid': True,
             'lines.markersize': 8, 'lines.linewidth': 2,
             'font.size': 14}
plt.rcParams.update(newparams)

def f(x):                   # definerer funksjonen i eksempelet over
    return x**2-2

# plotter funksjonen på et intervall 
x = np.linspace(-2, 2, 101)     # antall x-verdier i intervallet [-2,2]
plt.plot(x, f(x))               # plotter funksjonen f(x) i blått
plt.plot(x, 0*x, 'r')           # plotter x-aksen i rødt
plt.xlabel('x')
plt.grid(True)
plt.ylabel('f(x)');

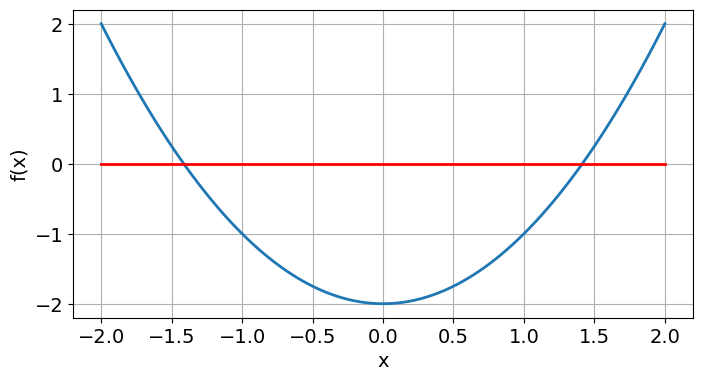
I følge plottet bør funksjonen \(f(x)\) ha 2 røtter, og disse er \(x=-\sqrt{2}\) og \(x=\sqrt{2}\).

Hvordan finner vi disse numerisk?

Fikspunktiterasjoner

Vi sier at \(x_0\) er et fikspunkt til \(F(x)\) dersom

\[ F(x_0)=x_0. \]

Eksempel

Definer

\[ F(x)=\frac{1}{2}\left(x+\frac{2}{x}\right). \]

Vi ser at \(f(x)=0\) og \(F(x)=x\) har samme løsningsmengde for \(x>0\) siden

\[ x=\frac{1}{2}\left(x+\frac{2}{x}\right)\qquad\Longrightarrow\qquad x^2-2=0. \]

Vi definerer nå følgen \(\{a_n\}_{n=0}^{\infty}\subseteq \mathbb{R}\) til å være gitt rekursivt som

\[ a_{n+1}=F(a_n),\qquad\text{med startverdien $a_0$,} \]

og vi skal se at denne konvergerer mot \(\sqrt{2}\). Legg merke til at \(F(\sqrt{2})=\sqrt{2}\).

import numpy as np

# generisk iterativ fikspunktmetode
def fikspunkt(F, a, toleranse = 1.0E-10, N = 500):
    Fa = F(a)
    n = 0
    punkter = [(a, Fa)] 
    while abs(Fa-a) >= toleranse and n < N: # vi gjør dette mens |F(x)-x|<toleranse og n<N
        a = F(a)   # ny startverdi
        n = n+1    # ny n
        Fa = F(a)  # ny F(x)
        punkter.append((a, Fa))
    if n >= N:
        print("Fant ikke fikspunkt for gitt startverdi. Returnerer nåværende verdier.")
        return Fa, punkter
    else: 
        return Fa, punkter

# definerer funksjonen vi skal bruke
def F(x):
    return 0.5*(x+(2/x))

# finner fikspunkt med gitt startverdi
svar, punkter = fikspunkt(F, 9)

# skriver ut punkter
for punkt in punkter:
    print('x = {:1.15f}\t F(x) = {:1.15f}'.format(*punkt))

x = 9.000000000000000	 F(x) = 4.611111111111111
x = 4.611111111111111	 F(x) = 2.522423025435073
x = 2.522423025435073	 F(x) = 1.657655721288586
x = 1.657655721288586	 F(x) = 1.432089434900886
x = 1.432089434900886	 F(x) = 1.414325129015109
x = 1.414325129015109	 F(x) = 1.414213566773468
x = 1.414213566773468	 F(x) = 1.414213562373095
x = 1.414213562373095	 F(x) = 1.414213562373095

Vi kan også visualisere dette geometrisk.

import numpy as np
import matplotlib.pyplot as plt

x = np.arange(0.05, 10.05, 0.01) # lager mesh for grafer på en annen måte enn tidligere

# fikspunktet inntreffer når følgende grafer skjærer hverandre
plt.plot(x, F(x), 'b') # plotter F(x) i blått 
plt.plot(x, x, 'r')    # plotter y = x i rødt

# visualiser fikspunktiterasjonen i grønt
for x, y in punkter:
    plt.plot([x, x], [x, y], 'g') # lager vertikal linje mellom punktene (x,x) og (x,y)
    plt.plot([x, y], [y, y], 'g') # lager horisontal linje mellom punktene (x,y) og (y,y)
plt.show()

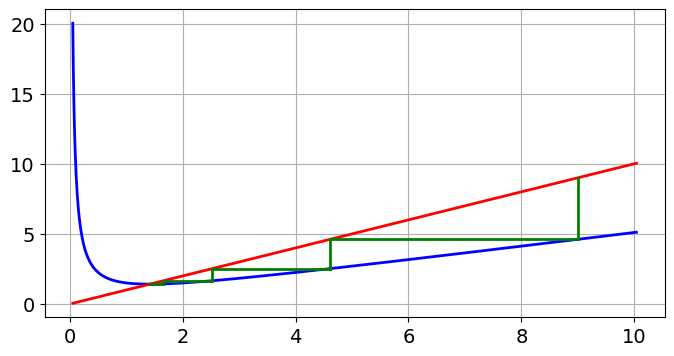
Hvis \(a_0>\sqrt{2}\), kan vi vise at \(a_{n}>\sqrt{2}\) og \(a_{n+1}\leq a_{n}\) for alle \(n\geq0\). Dermed konvergerer \(\{a_n\}_{n=0}^{\infty}\) og \(\lim_{n\to\infty} a_n=\sqrt{2}\).

Hvorfor må grenseverdien være \(\sqrt{2}\)?